ÁLGEBRA OCTAVO

Congruencia

Dos objetos geométricos son congruentes si tienen las mismas medidas y los mismos ángulos.

Por ejemplo, los siguientes segmentos son congruentes:

Igualmente, los siguiente dos ángulos son congruentes, pues tienen la misma medida:

Los siguientes triángulos son congruentes, pues tienen las medidas de sus lados y de sus angulos iguales, uno a uno:

Para denotar matemáticamente que los triángulos $\triangle ABC$ y $\triangle A'B'C'$ son congruentes, vamos a usar la notación:

$\begin{equation*} \triangle ABC \cong \triangle A'B'C' \end{equation*}$

y esto se leerá como: El triángulo $ABC$ es congruente con el triángulo $A'B'C'$ .

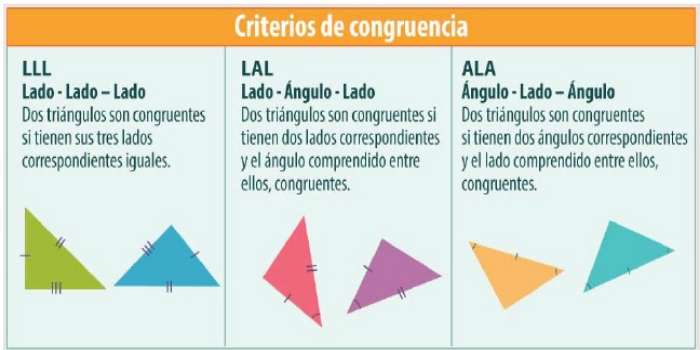
Existen tres criterios para determinar si dos triángulos dados son o no congruentes.

Los criterios son los siguientes:

(i) Si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, los dos triángulos son congruentes.
(ii) Si un ángulo de un triángulo es congruente con el ángulo de otro triángulo, y además los lados del ángulo considerado en cada triángulo son congruentes, entonces los dos triángulos son congruentes.
(iii) Si las longitudes de los lados de un triángulo son congruentes a las longitudes de los lados de otro triángulo, entonces los dos triángulos son congruentes.

Resultado de imagen de criterios de congruencia de triangulos

Semejanza de figuras

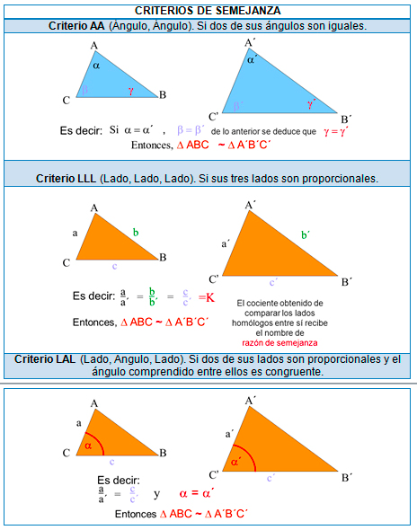
Dos figuras geométricas son semejantes si tienen los mismos ángulos internos (uno a uno) y sus lados correspondientes tienen la misma proporción.

Cuando decimos que dos figuras son semejantes queremos decir que ambas tienen la misma forma, pero tal vez una es escala de la otra. Los siguientes dos triángulos son semejantes: